A PID (Proportional-Integral-Derivative) controller is a controlling mechanism which enables to regulate in a closed loop via an automatic system. It is the type of regulator the most used in the industrial field which enables to control many processes.
Let's see a story to understand the regulation principle
Imagine that you are driving your car on the highway and you wish to stabilise your speed at 80 mph. In practice, you will succeed easily. In this example, it is important to understand how your mind manages to regulate your speed intuitively.
Rule n°1: Proportional control
First of all, the thing you do intuitively when you have to drive at a certain speed is “the more I drive slowly compared to the speed I want, the more I press the accelerator pedal”. The pressing on the accelerator is then proportional to the error that you commit. In other words, proportional to the difference between the desired speed and the real speed.
With this method, if you are at 30 mph; you push the accelerator pedal down fully. Your speed rises quickly and gets closer to the limit speed. Once the speed gets to 80 mph, the error becomes null and then you release the accelerator. Thereafter, with the inertial effect, we exceeded the required speed.
Releasing the accelerator causes the car to slow down until it goes under the desired speed. Thus, you start again to push the accelerator, and then gradually more to reach 80 mph. Finally, you manage to stabilise your speed at a lower speed than the desired one, let’s say 70 mph.
Rule n°2: Integral control
And then you think: “Shoot! I cannot manage to reach the desired speed. I need to add another rule to my thinking!” So, you decide that if your speed stays for a long time below the objective, you accelerate more and more. So you decide that besides accelerating proportionally to the error committed, you thus memorise it over time. The more the total error is important, the more you accelerate.
Thus, when you stabilise your speed at 70 mph, the total error rises and you push harder and harder on the accelerator until reaching 80 mph and exceed it! In fact, at 80 mph, the total error is positive, so you keep pushing on the accelerator.
Over 80 mph, the error is negative and the total error decreases. You take your foot off the pedal ever more strongly until reaching back 80 mph. Once at 80 mph, same thing again, the error is negative and you continue to slow down. So you accelarate and so on and so forth until you finally manage to stabilise at 80 mph after several oscillations.
Rule n°3: Derivative control
At 80 mph, you think “there it is! But I wasn’t really effective… Should I add a third rule to be more effective?” So you decide to anticipate your speed. The more your speed gets closer to the optimal speed, the less you accelerate and the less it reaches the optimal speed, the more you accelerate!
Then, you rapidly get closer to 80 mph, you quickly remove your foot to not get over the 80 mph too brutally. By anticipating, we reduce the phenomenon of oscillations and you rapidly stabilise to the desired speed!
There it is, you intuitively made a PID regulation!
General principle
The error observed is the difference between the setpoint and the direct measure.
PID causes 3 actions according to this error:
- Proportional: the error is multiplied by a G gain
- Integral: the error is integrated on a S time interval, then multiplied by a Ti gain.
- Derivative: the error is derived following a time, and then multiplied by a Td gain.
It exists several architectures possible to combine the 3 effects (serial, parallel or mixed).
The example presented below is a parallel-type achitecture which is the most widespread.
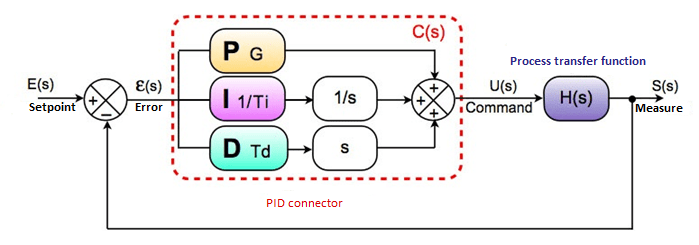
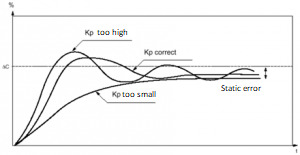
1) Proportional control:
The proportional action enables to influence the process response speed.
The more the gain is high, the more the response gets fast, the more the static error diminishes (in pure proportional), but the more the stability deteriorates.
Then, it is necessary to find a good compromise between speed and stability.
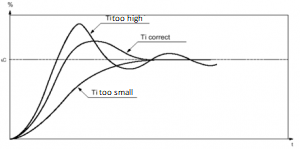
2) Integral control:
The integral action enables to cancel the static error (the difference between the measure and the setpoint).
The more the integral action is high (Ti small), the more the response gets fast and the more the stability deteriorates.
Here too, it is necessary to find a good compromise between speed and stability.
3) Derivative control:
The derivative action is proactive. In fact, it adds an element that takes into account the gap variation speed. It enables to anticipate by accelerating the response of the process when the gap gets larger. On the contrary, by slowing it when the gap diminishes.
The more the derivative action is high (Td high), the more the response gets fast.
Here again, it is necessary to find a good compromise between speed and stability.

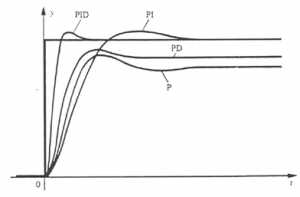
4) Proportional, Integral, Derivative (PID) control:
This figure highlights the action of each corrector by the same control system.
- ensures rapidity: action P
- cancels the static error: action I
- improves stability: action D
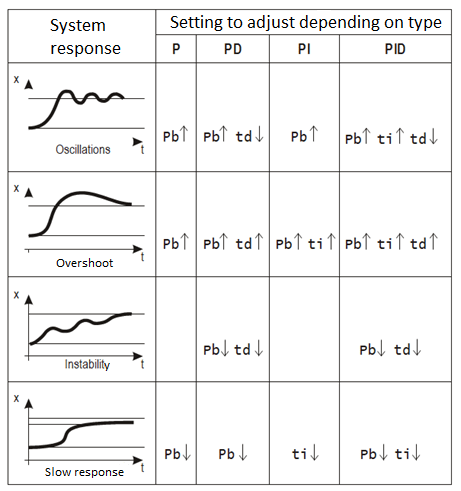
PID parameter setting method:
Manual method:
- If the system must stay in production, a setting method consists in putting the values Integral (I) and Derivative (D) at zero.
- Then, increase the Proportional (P) gain until the output oscillates.
- Finally, increase the gain of the Integral until the oscillation stops.


 Blog
Blog

